平衡树

(Updated: )
面试 › 数据结构与算法

概述

为解决二叉搜索树退化成一张链表的情况，改进出了AVL（取名与作者G.M.Adelson-Velsky和E.M.Landis）

一颗AVL具备的条件：

  • 必须是一颗BST
  • 每个节点的左右子树高度至多相差1

AVL树的查找、插入、删除等操作在平均和最坏的情况下都是O(logN)，得益于其一直在动态的维护平衡性

相关参数

  • 平衡因子

    左子树高度减去右子树高度的值称为该节点的平衡因子BF(Balance Factor)。若BF的绝对值大于1，则表明需要进行调整

  • 最小不平衡子树

    距离插入节点最近的，且平衡因子的绝对值大于1的节点为根的子树

调整方式

  • LL型

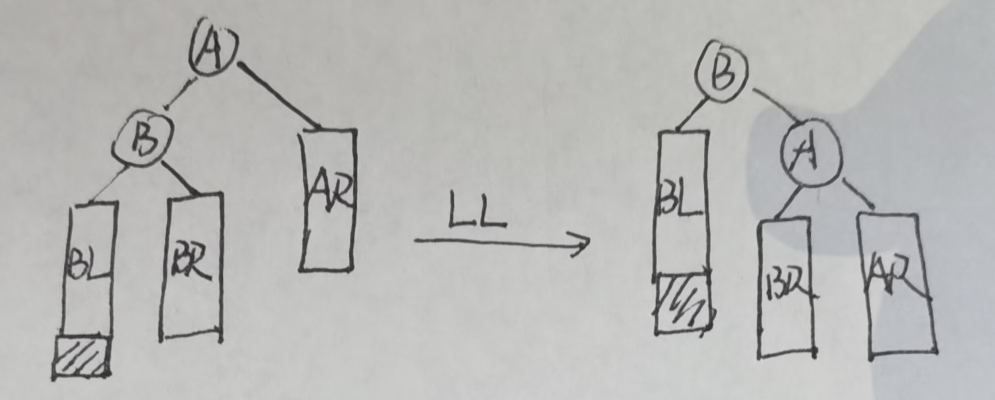
    image-20220723165252254

  • RR型

    image-20220723165416390

  • LR型

    image-20220723165429874

  • RL型

    image-20220723165447301

其中LL和RR型就可以看成将中间的节点”拎起来“

LR和RL型就先将拐出来的部分旋转为LL和RR型，再进行对应的操作

代码实现

LL型平衡

1
2
3
4
5
6
private Node<T> llRotate(Node<T> avlNode) {
        Node<T> node = avlNode.leftChild;
        avlNode.leftChild = node.rightChild;
        node.rightChild = avlNode;
        return node;
}

RR型平衡

1
2
3
4
5
6
private Node<T> rrRotate(Node<T> avlNode) {
        Node<T> node = avlNode.rightChild;
        avlNode.rightChild = node.leftChild;
        node.leftChild = avlNode;
        return node;
}

LR型平衡

1
2
3
4
private Node<T> lrRotate(Node<T> avlNode) {
        avlNode.leftChild = rrRotate(avlNode.leftChild);
        return llRotate(avlNode);
}

RL型平衡

1
2
3
4
private Node<T> rlRotate(Node<T> avlNode) {
        avlNode.rightChild = llRotate(avlNode.rightChild);
        return rrRotate(avlNode);
}

平衡实现逻辑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
private Node<T> balance(Node<T> node) {
    // 左子树比右子树高度大于1以上
    if (getAvlTreeHeight(node.leftChild) - getAvlTreeHeight(node.rightChild) > 1) {
        if (getAvlTreeHeight(node.leftChild.leftChild) >= getAvlTreeHeight(node.leftChild.rightChild)) {
            // 执行LL型调整
            node = llRotate(node);
        } else {
            // 执行LR型调整
            node = lrRotate(node);
        }
    } else if (getAvlTreeHeight(node.rightChild) - getAvlTreeHeight(node.leftChild) > 1) {
        if (getAvlTreeHeight(node.rightChild.rightChild) >= getAvlTreeHeight(node.rightChild.leftChild)) {
            // 执行RR型调整
            node = rrRotate(node);
        } else {
            // 执行RL型调整
            node = rlRotate(node);
        }
    }
    return node;
}

建立AVL逻辑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public void createTree(T data) {
    if (data == null) {
        return;
    }
    root = insert(root, data);
}

private Node<T> insert(Node<T> root, T data) {
    // 根节点为空，说明树为空，则创建一颗树
    if (root == null) {
        return new Node<>(data);
    } else {
        if (compare(root, data) > 0) {
            root.leftChild = insert(root.leftChild, data);
            root = balance(root);
        } else if (compare(root, data) < 0) {
            root.rightChild = insert(root.rightChild, data);
            root = balance(root);
        }
        return root;
    }
}

功能测试

1
2
3
4
5
6
7
8
9
10
private static final Integer[] arrays = new Integer[]{26, 21, 30, 50, 60, 66, 68, 70};

@Test
public void createAvlTree() {
    AvlTree<Integer> avlTree = new AvlTree<>();
    for (Integer data : arrays) {
        avlTree.createTree(data);
    }
    avlTree.printTree();
}
1
2
3
前序遍历： 26 21 66 50 30 60 68 70 
中序遍历： 21 26 30 50 60 66 68 70 
后序遍历： 21 30 60 50 70 68 66 26

代价分析

  • 查找：效率很好，平均情况和最坏情况都是O(logN)
  • 插入：每插入一个节点至多需要旋一次旋转。总体时间复杂度为O(logN)
  • 删除：每一次删除最多需要O(logN)次旋转，复杂度为O(logN)

AVL树的结构相当的稳定，故查询效率相当的高。但每次插入或删除节点时都会进行动态的维护平衡，带来了不小i的时间成本。所以当查询和删除频率不高时，采用AVL树可以带来极高的查询效率。但当插入和删除频率较高时，AVL的性能并不理想，此时，我们选择采用红黑树

相关代码可以在 https://github.com/Cheung0-bit/tree-practice 中找到